One of the common issues posed in the practice of civil engineering is how to estimate the volume of holes - porous volume - between more or less regular solid particles. Sometimes this hot topic originates long debates with reluctant contractors and picky consultants.
Recently, I have needed to give a number for the spare space in a stone wall like that in the image below. In the project, the interstitial space was required to be filled with cement mortar until certain height to ensure the stability of the base. A bit of mathematics and Wikipedia were useful to justify the necessary amount of the concrete.
Left: Masonry wall in a Roman path somewhere in Germany. Right: Well, needless to say that those are oranges.
The majority of the stones in a wall have similar weight and appearance and, in fact, they are usually defined by a characteristic diameter. If we assume that stones are like oranges -I mean spheres- and that the maximum density of packaging is achieved, the problem can be transformed into the Kepler's conjecture that was proved by Prof. Thomas Hales a decade ago.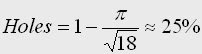 It is clear that stones are not spheres -ellipsoids would be a better approximation- but this value of the porosity is close to experiments referred for coarse non-graded gravel in several books. At least, if the on-site engineer asks for the origin of the famous 25% of holes I will have something interesting to say.
It is clear that stones are not spheres -ellipsoids would be a better approximation- but this value of the porosity is close to experiments referred for coarse non-graded gravel in several books. At least, if the on-site engineer asks for the origin of the famous 25% of holes I will have something interesting to say.
Structures, water, computers, languages and people (not necessarily in this order)
Packaging of stones
Subscribe to:
Post Comments (Atom)

Ah, the beautiful world of the packing problems :) Even if that answer must be more than sufficiently accurate for your purpose, I presume the problem must become quite complicated when you start thinking in terms of the distribution of sizes of the oranges, I mean, stones.
ReplyDeleteSo the proof transfroms Kepler's conjecture into T.Hales' Theorem!!
ReplyDeleteInteresting topic. I imagine David is right and it gets even more interesting when you try to find the distribution of diameters that gives you the highest compacity. (Of course subject to a constraint in the smallest diameter you can use or something like that, otherwise a monkey could get holes=0%).
In that case I wonder how it would compare to Füller and Bolomey.
Hales's Holes' Theorem?
ReplyDelete:-S
Off-topic: One of the items showing in News at iCivilEngineer on the right navigation bar of this blog, "River plants may play major role in health of ocean coastal waters", refers to research being done in our Fluids Group at MIT :)
ReplyDeleteMay I "put my little grain of sand" (or add my two cents -of sand-, if you prefer)?
ReplyDeleteIf we have 1kg of of gravel with diameter 1 and we add 20/4*(1/3)^3 kg of gravel with d=1/3 plus 20*(1/6)^3 kg of gravel with d=1/6 we get a density of packing of 94.62% (if I'm not mistaken). Is that interesting?
Iago, how do you calculate that? Do you:
ReplyDelete(1) place the largest spheres in close packing,
(2) look at the geometry of the holes between those,
(3) compute how many spheres of the next size you can put in close packing in those holes,
(4) go to (2)
?
If you follow this procedure (which may not be optimal), I would expect the diameters to form a geometric series (1,1/3,1/9,...). How did you come up with 1/6 for the third diameter?
Exactly. Yes, I am not saying that it is an optimal solution (of course, the problem is too complicated to be solved during my break!! :) )
ReplyDeleteI just wanted to get "a value".
Yes, you put the spheres, and then you see that you can place another sphere of d=1/3 in the holes. Once the holes are filled the biggest sphere you can put is of d=1/6. It is not a geometric progression because the last sphere touches 2 of the d=1/3 spheres and also 3 of the d=1/6. So you are not repiting the same pattern.
If you want to find the next d you can fit, you are welcome, but the calculations start to get cumbersome. Good luck!!
I see... Well, at least I can say that the next d is grater than or equal to d=1/9, which is the diameter I can fit in the holes of the d=1/3 spheres :)
ReplyDeleteSorry, I didn't get that. A priori, the next diameter could be greater, equal or less than 1/9, because you are not filling the holes of the d=1/3 spheres: They are not in contact to each other.
ReplyDeleteBy the way, my number is optimal in some way: Given the amounts of material that I said and the diameters I chose, the maximum density we can get is 94.62% (unless I'm mistaken, of course).
But as I said before, in order to talk about an optimal solution with different diameters we would first need some constraints, otherwise the problem is not well posed and the 100% is easily attainable.
Oh, sorry, I forgot that you only have one d=1/3 sphere between the large ones. You are right.
ReplyDeleteApreciado Xosé,
ReplyDeleteGrazas polo que me dis no meu blog. Pensa que eu estudei na UNED fai xa uns 10 anos ou mais, co cual me imaxino que as cousas mudarán.
Se queres irme visitando, xa sabes. Eu leo regularmente Vieiros.
Até pronto,
martí
its great.
ReplyDeletePile Repairs
Waterproofing