Reinforcement that is not perperdicular or that is arranged in more than two directions occurs frequently in the design of slabs for skew bridges. In such cases, reinforcement can be calculated with an equivalent orthogonal reinforcement.
Given n arbitrarily oriented groups of paralel bars r1, r2, ...., rn, an equivalent reinforcement (ru, rv, ruv) for an auxiliar set UV of perpendicular axes are obtained by projection:
ru = r1*(cos(a1))^2 + ... + rn*(cos(an))^2
rv = r1*(sin(a1))^2 + ... + rn*(sin(an))^2
ruv = r1*cos(a1)sin(a1) + ... + rn*cos(an)sin(an)
These values are transformed into the principal directions of reinforcement XY (that are obviously orthogonal) like this:
rx = ru*(cos(b))^2+rv*(sin(b))^2+ruv*sin(2*b)
ry = rv*(sin(b))^2+rv*(cos(b))^2-ruv*sin(2*b)
where
b= 0.5*arctan(2*ruv/(ru-rv))
Now, the axial and flexural resistance should be confronted with the forces and moments given in the XY system of coordinates. Changing the local axis of the shell elements we obtain Nx, Ny, Nxy and Mx, My, Mxy.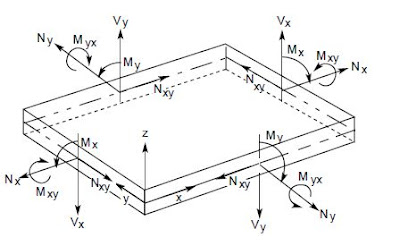 The Wood and Armer rule (or any other similar) can be applied now.
The Wood and Armer rule (or any other similar) can be applied now.
rx should resist Nx' and Mx'
ry should resist Ny' and My'
For a symmetric ultimate reinforcement with Nxy and Mxy not extremely large, Wood and Armer rule becomes.
Nx' = Nx +/- |Nxy|
Ny' = Ny +/- |Nxy|
Mx' = Mx + sign(Mx)*|Mxy|
My' = My + sign(My)*|Mxy|
Structures, water, computers, languages and people (not necessarily in this order)
The skew (or non-orthogonal) reinforcement problem
Subscribe to:
Post Comments (Atom)

Wood and Armer does not always give an appropriate result, as it can be too conservative i.e. okay for design but not really for appraisal of existing bridge decks. The paper by Denton and Burgoyne is better in many respects - see http://www-civ.eng.cam.ac.uk/cjb/papers/p33.pdf
ReplyDeleteGood comment. I've heard about about Denton&Burgoyne rule and its goodness but I must confess that I have never applied it to real projects.
ReplyDeleteThe assesment of existing bridges is another matter: unfortunately, an existing bridge can work well even if one is unable to find a sophisticated nonlinear computer model that justifies the resistance of the bridge. And this is difficult to explain to any client.